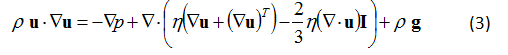So far we have explored preliminary ways to predict the temperatures in a circuit using simple thermal resistance network calculations. This post addresses improved thermal analysis for electronics cooling. Consistent exposure to high operating temperatures can lead to degradation of material properties and development of thermal stresses that can ultimately lead to device failure. The relationship between reliability and the operating temperature of a typical silicon semiconductor device shows that an increase in operating temperature corresponds to an exponential decrease in reliability and life expectancy of the device it is essential that the operating temperatures are maintained at specific levels.
To reduce the temperatures to an acceptable level three approaches are generally considered:
- Reconfigure the components, power settings and operating conditions to reduce the temperatures,
- Refine the thermal calculation to develop a more accurate prediction of the temperature distribution, or
- Identify potential mitigation techniques
The first option is at the discretion of the circuit and application designers and is therefore beyond the scope of these Blogs so let’s examine ways to improve the accuracy of the temperature calculation to make sure we can remain in the allocated thermal budget. While it is tempting to add complexity to the thermal resistance approach by adding more thermal resistance pathways this step alone will not increase the accuracy to the level required. As we have seen the inherent assumptions in the thermal resistance network approach, for example the use of convection coefficients, can significantly affect the accuracy of the solution.
Two other approaches of thermal analysis for electronics cooling exist that can provide a more accurate assessment of the thermal profile of a power electronics circuit. First, Green function formulations simplify the problem to two dimensional modeling and are consequently fast but provide limited accuracy. Secondly, predictive physics based computational simulation techniques using finite difference, finite element or boundary–element techniques can explicitly solve heat transfer due to combined conduction, convection and radiation. These techniques provide high accuracy, incorporate multiple, independent heat sources and apply different boundary conditions to provide an accurate representation of a circuit’s behavior. The main drawbacks of these approaches are that the complexity of the problem set up often requires use by skilled personnel and they may require specific computational hardware to deal with the size of the analysis files. Despite these problems computational thermal analysis of power electronics circuits is widely available and provides critical information to alleviate thermal management problems.
Traditionally predictive physics based computational approaches have been used to analyze behavior at the system level when problems exist that may be too deeply ingrained to provide an optimum solution. Integration of computational analysis earlier in the concept and prototype phases can not only lead to improved performance but can also accelerate the rate at which products are developed. Generally computational analysis can be valuable in the following stages of product development:
1) Concept
- Little detail of the circuit of component may be known but this allows the development of thermal analyses that are simple and quick to implement while still providing valuable information and advanced warning about potential problems. Features and layout can be examined at a stage in the product development where limited investment has been made so that costs for any required changes are minimal.
2) Prototype
- Components may be represented by isolated blocks with assigned powers and details of board construction and leads may be simplified by using averaged properties. Individual material properties and thermal resistances for the components will generally be assigned at this stage.
3) Final design
- Construction details of the board and components are typically included such that copper layers or thermal vias in the board are discretely identified, and individual construction details of the components including leads, solder balls and connectivity to the PCB. This analysis provides the most detailed description of the thermal behavior of the product of interest and most likely will require significant computational resources and time to complete the analysis.
The process of developing a predictive analysis involves the following steps:
- Geometry development
- Assign material properties
- Develop discrete mesh
- Integrate relevant physics and inputs
- Apply boundary conditions
- Solve the problem
- Analyze the results
- Modify set up to address problems or optimize design and operation
Virtual representation of the circuit by is obtained by discretizing the components into domains each having their respective geometric shape and spatial location, e.g. Figure 1. Some simplification or defeaturing of the geometry may be performed on features having no effect on the analysis or components not influencing behavior may be eliminated, eg fillets, fasteners and labels, while maintaining individual control over critical aspects of the geometry, eg vent size, spacing, pitch, shape etc.
Figure 1: Example of component geometry and surrounding spatial volume.
Connectivity between the various components is maintained and individual materials properties that may be a function of temperature are assigned to the respective components. Details such as individual copper layer, vias or interconnects can be defined if needed but it must be realized that inclusion of these details may affect the computational resources needed to run the model and may only be needed for more detailed assessments. Isolated powers are applied to individual components as defined by the device operation and the analysis can be set up to include any combination of thermal transfer due to conduction and radiation or fluid flow of the type needed to solve heat transfer due to convection
As the components heat up the heated fluid at the surface has a lower density and thus rises creating a natural convection current. The surrounding cooler fluid then moves to replace it thus creating a buoyancy effect. This cooler fluid is then heated and the process continues transferring heat energy from the bottom of the convection cell to the top. Alternatively air may be forced to flow over the components by fans producing defined flow rates.
Heat transfer within the solid domain is described by the standard heat equation:
where, ρ is the density of the solid or fluid material, cp is the specific heat capacity, T is the temperature, and λ is the thermal conductivity.
In the fluid domain, the physics are described by the conservation of mass, momentum, and energy according to the following equations:
The viscous heating and pressure work terms are neglected in the energy equation. In the above equations, ρ is the density, u is the velocity vector, p is the pressure, η is the dynamic viscosity, g is the gravitational acceleration vector, k is the thermal conductivity, T is the temperature, Q is a heat source term, and cp is the specific heat capacity. The viscosity, thermal conductivity, and specific heat capacity are functions of temperature, while the density is a function of both temperature and pressure. The heat flux at the surface of the part due to radiation is modeled by:
where εemis is the emissivity of the surface, Gm is the mutual irradiation from other surfaces, Famb is the ambient view factor, σ is the Stefan-Boltzmann constant, Tamb is the far-away ambient temperature, and T is the temperature at the surface. Gm is a function of the radiosity. In the presence of mutually irradiating surfaces, the ambient view factor and mutual irradiation can be automatically computed by most computational analysis packages.
Results of the analyses can provide significant information and understanding about the distribution of thermal energy in the circuit and the flow of air resulting from any natural or forced convection, e.g Figures 2 and 3. The effectiveness of potential solutions to problems can be rapidly evaluated by inserting additional features or heat conduction paths to identify the resultant thermal distribution.
Figure 2: Surface temperature distribution
Figure 3: Air flow velocity
Further refinement of the analysis can also provide valuable information about component case and junction temperatures that can aid in the design and development of appropriate heat dissipation techniques to ensure that operational conditions are maintained in the required range. Details of the individual component or board construction including leads and solder balls in the chips, and copper vias and planes in the board can also be integrated to provide a detailed analysis of the final design and identification of localized behavior. The more detailed the analysis the more accurate the temperature predictions but also the more complex the analysis is to set up.
Once properly calibrated and validated computational procedures have been developed the results of the analyses can be used to optimize designs and operating procedures with much greater tolerances than the preliminary resistance network procedures discussed in earlier Blogs. Alternatively trends and sensitivities can be easily explored to allow the effect of changes in design to be identified without the need to retrofit operational components with last minute fixes to problems uncovered in traditional testing and evaluation approaches. The higher level of fidelity and accuracy obtained with these computational approaches allows safe component and device operation close to the boundaries of the established thermal budget and a more comprehensive exploration of the safe operating space. Future Blogs will look at mechanisms to dissipate heat when normal operating temperatures exceed recommended values.
Please feel free to contact us if you have questions about thermal analysis for electronics or feasibility studies in general, or if you would like to discuss thermal aspects of your application.