The fast-growing area of acoustic metamaterials, specifically those composed of subwavelength periodic artificial structures with specific designs, has drawn significant research attention. In this article, we compare acoustic metamaterials to the limitations of conventional acoustic materials in sound absorption, and what we discover is acoustic metamaterials are far more effective for low-frequency applications.
LIMITATIONS OF CONVENTIONAL ACOUSTIC MATERIALS
It is well known that conventional materials can only provide high transmission loss at relatively high frequencies over 1 kHz, and fail to efficiently absorb sound at lower frequencies, which is a direct consequence of the mass-frequency law (for a detailed discussion on sound transmission in traditional materials, see appendix).
Some resonator absorbers can provide effective absorption at low frequencies. However, this absorption is limited to a few of its resonant frequencies, and still, their absorption magnitude is low. Thus, conventional materials cannot completely absorb or reflect sound, especially in the range of 100 Hz to 1 kHz, which is the most difficult range for noise control.
ACOUSTIC METAMATERIALS CHARACTERISTICS
To overcome the limitations of conventional acoustic materials following the mass-frequency law, new materials have been designed that can control, direct, and manipulate sound waves like no naturally occurring materials. These new materials are called acoustic metamaterials.
Acoustic metamaterials are artificial materials that are comprised of sub-wavelength microstructures, called unit cells, that are designed to manipulate sound waves in a manner not found in conventional acoustic materials. This extraordinary wave manipulation is achieved by controlling the bulk acoustic properties, such as effective bulk modulus (Beff) and effective mass density (Peff). Acoustic metamaterials are also used to model and research extremely large-scale acoustic phenomena like seismic waves and earthquakes[1], as well as extremely small-scale phenomena like atoms.
ACOUSTIC METAMATERIALS IN ACTION
Now that we have explained what an acoustic metamaterial is, we’d like to turn our focus to a recent project by AltaSim Technologies to determine if sound is absorbed more efficiently at lower frequencies with acoustic metamaterials or traditional materials.
What you will see in this article are some basic ideas behind acoustic metamaterials that represent subwavelength artificial periodic structures that possess extraordinary acoustic properties. We explain this through:
- Identifying the schematic of acoustic metamaterial as a periodic arrangement of unit cells
- Using the transmission of sound through plate and semi-heuristic derivation of mass-frequency law to demonstrate that conventional materials fail to efficiently absorb sound at lower frequencies
- Looking at the historically first proposed membrane-type model for acoustic metamaterials
- Deriving the equation of acoustic vibrations for this model and demonstrating that such artificial material exhibits negative effective mass density over the broad range of low frequencies. Hence it breaks the mass-frequency law of conventional materials and acts as a perfect sound absorber in the broadband region of its negative effective mass density.
- Considering a numerical example of periodic structure acting as an acoustic bandgap filter. The unit cell of this filter represents membrane-type acoustic metamaterial combined with the Helmholtz resonator.
SCHEMATIC OF ACOUSTIC METAMATERIAL AS A PERIODIC ARRANGEMENT OF UNIT CELLS
Current advances in acoustic metamaterial research and development are related to theoretical studies and fabrication approaches including additive manufacturing. Research and advancements in these areas have been significantly aided by fast-growing computer modeling and simulation.
Figure 1. Schematic of acoustic metamaterial as a periodic arrangement of unit cells and its representation as a homogeneous material with effective bulk acoustic properties.
The schematic of the unit cell and its homogeneous representation is shown in Figure 1. The unit cell is made of conventional materials with conventional values of bulk effective modulus B and density p. However, due to the shape, geometry, and arrangement of the unit cells, the overall material may behave as homogeneous material with effective bulk properties not found in nature.
If the equivalent homogeneous medium has either negative effective bulk modulus, 
, or negative effective density, 
, then speed of sound and wavenumber in such media become complex-valued:
Materials with negative effective mass density or negative effective bulk modulus are called acoustic metamaterials.
Consider a pressure plane wave traveling in the x- direction:
When we substitute a complex-valued wavenumber into the equation for plane wave, we obtain:
This shows the wave does not propagate over space but exponentially decays. A medium with a negative effective mass density or negative bulk modulus does not allow acoustic wave propagation. Wave propagation is such a medium that does not obey the mass-frequency law. Most acoustic metamaterials use the principle of negative density or negative bulk modulus to attenuate and manipulate the propagation direction of sound waves.
MEMBRANE-TYPE ACOUSTIC METAMATERIALS
The concept of membrane-type acoustic metamaterials was proposed by Yang et al. 2008[2]. This type of acoustic metamaterial contains a limp membrane as a primary construction element in the unit cell. A vibrational response of a membrane depends on the applied tension and can be tuned to provide a sound total absorption or total reflection.
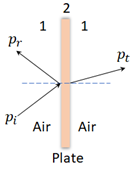
Here we have developed a simplified model for membrane-type acoustic metamaterial following Lee et al 2009[3]. The unit cell is a membrane clamped inside a subwavelength waveguide and subjected to an incident plane wave, as shown in Figure 2.
Figure 2. Unit cell of membrane-type acoustic metamaterial.
The membrane behaves as a spring, and exerts a restoring force, Fm, due to its tension to bring it back to equilibrium position:
Acoustic force acting on a membrane is due to the incident pressure wave and can be expressed as:
Total mass of the unit cell is superposition of air mass inside cell and membrane mass:
In the above equations, we are using the following notations:
Fm : membrane restoring force
Km : membrane stiffness
A : membrane surface area
Mm : membrane mass
w : membrane transverse displacement
Pa : air density
d : length of unit cell
p: pressure acting on faces of unit cell
Equation of motion of unit cell is written based on the Newton’s law:
or
For the plane harmonic wave we have the following relations:
Thus, the equation of motion is written as:
where the following notations were used:
After additional manipulation, and introducing notation
for natural angular frequency of the unit cell, the equation of motion can be rewritten as following:
The last equation can also be written as
where Peff effective mass density of the unit cell.
From the last equation we conclude that the unit cell of membrane-type acoustic metamaterial has negative effective density in a broadband frequency range 
below a critical frequency 
that depends on the membrane tension, membrane surface density and membrane thickness, and mass of acoustic medium in the unit cell. In this wide region of negative effective mass density, the membrane-type unit cell does not allow any acoustic wave propagation and acts as a perfect sound absorber, as schematically shown in Figure 3.
Figure 3. Transmittance of membrane type acoustic metamaterial: acoustic wave does not propagate through unit cell in the frequency range below a critical frequency ω_0.
NUMERICAL EXAMPLE: ACOUSTIC METAMATERIAL BANDGAP FILTER
Over the last two decades various design has been proposed and developed for operation over a very wide frequency range starting from conventional frequency of 100 Hz and up to the near-megahertz frequencies for biomedical ultrasound applications[4]. Unit cells of acoustic metamaterial with negative effective mass density 
and positive effective bulk modulus are typically membranes or coated-bead structures. Metamaterials with negative effective bulk modulus 
and positive effective mass density can be obtained with open or closed cavity resonators. Unit cells with space-coiling or coupled filter-element structures produce double-negative 
metamaterials[5],[6].
We consider the example of membrane-type acoustic metamaterial with Helmholtz resonators by developing simulations using COMSOL Multiphysics v6.2. The unit cell shown in Figure 4a consists of a circular channel, prestressed membrane, and attached closed cavity. The diameter of the air channel is 3.5 cm. Prestress of the silicon membrane is 1.5 M Pa. Unit cells are stacked on top of each other to control acoustic properties. A stack of several unit cells is shown in Figure 4b.
Figure 4. Membrane type AMM with Helmholtz resonators. Unit cell (a), and stack of five cells (b).
Transmittance of the acoustic metamaterial structure is shown in Figure 5. The structure is excited by the acoustic plane wave traveling along the length of the circular channel. Transmittance is defined as a ratio of power transmitted by waveguide to the excitation power. A stack of multiple cells acts as an acoustic filter completely blocking sound over certain range of frequencies. Sound blocking frequency bandwidth and its location can be controlled by membrance stiffness and its prestress level, cell geometry, and number of unit cells in stack.
Figure 5. Transmittance of the AMM with Helmholtz resonators.
APPENDIX: SOUND TRANSMISSION IN TRADITIONAL MATERIALS
Sound Transmission Through Plate
Consider sound transmission through an infinitely large plate of thickness t. Assume that the stiffness of the plate is negligible compared to its mass, and the plate is homogeneous and solid.
Figure 6. Schematic of sound transmission through an infinitely large thin plate.
Consider air/plate interface. Acoustic pressure is harmonic function:
Acoustic particle velocity on the plate is also harmonic function:
By Newton’s second law, force acting on the plate
The same force can be expressed in terms of acoustic pressure:
From last two equations we find acoustic pressure:
Hence, specific acoustic impedance of the plate is
The following notations were used:
p: density of the plate
A: exposed surface area of the plate
t: thickness of the plate
M: mass of the plate
m: mass per unit area of the plate
Impedance for sound transmission through the plate is simply plate vibration plus impedance of fluid medium:
Air characteristic impedance is . Hence, we obtain the following impedance ratio:
Now we can calculate pressure reflection coefficient:
Mass-Frequency Law
The mass-frequency law describes the relation between sound frequency, mass per unit area, and sound insulation efficacy. In other words, a material with a higher density is less likely to vibrate when in contact with sound waves and will transmit less noise through the substrate.
Assuming no losses in air, sound transmission coefficient is calculated as:
Transmission loss in dB scale is given by
Impedance of the air is much greater than impedance of a massy plate:
Then sound transmission coefficient,
, and transmission loss, TL, can be expressed as
All traditional acoustic materials approximately satisfy the mass-frequency law:
where m is plate mass per unit area and f is incident frequency.
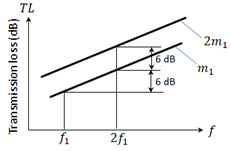
Mass-frequency law can also be formulated as: TL increases by 6 dB for every doubling of frequency. Also, TL increases by 6 dB for every doubling of surface mass density, as shown in Figure 7.
Figure 7. An ideal mass-frequency law curve for traditional materials.
References:
[1] Gupta, A., Sharma, R., Thakur, A., and Gulia, P., Metamaterial foundation for seismic wave attenuation for low and wide frequency band, Nature, (2023) 13:2293 (https://doi.org/10.1038/s41598-023-27678-1)
[2] Z. Yang, Jun Mei, Min Yang, N. H. Chan, and Ping Sheng, Membrane-Type Acoustic Metamaterial with Negative Dynamic Mass, Phys. Rev. Lett., 2008, 101, 204301
[3] Lee, S. H., Park, C. M., Seo, Y. M., Wang, Z. G., & Kim, C. K. (2009). Acoustic metamaterial with negative density. Physics Letters, Section A: General, Atomic and Solid State Physics, 373 (48), 4464-4469
[4] Wang, J., Allein, F., Boechler, N., Friend, J., and Vazquez-Mena, O. Design and Fabrication of Negative-Refractive-Index Metamaterial Unit Cells for Near-Megahertz Enhanced Acoustic Transmission in Biomedical Ultrasound, Physical Review Applied, 15, 024025 (2021)
[5] Cummer, S., Christensen, J. & Alu, A. Controlling sound with acoustic metamaterials. Nat Rev Mater 1, 16001 (2016).
[6] Sztyler, B., Strumillo, P., Acoustic Metamaterials, Archives of Acoustics, Vol. 47, No. 1, pp. 3–14 (2022).