Frequency domain simulation techniques are widely used to analyze the behavior of arbitrarily shaped objects and complex materials. One of the disadvantages of traditional frequency domain techniques, however, is the computational cost involved in obtaining solutions over a range of frequencies. Simulations have to be repeated at each frequency of interest to obtain a complete response over the required frequency range. For frequency dependent systems such as resonant structures, the number of simulations required to capture details of the resonant response can cause noticeable increases in the number of simulations. To adequately resolve narrow peaks in resonant behavior, further fine scale increments in frequencies may be required such that computational resources and time can escalate rapidly.
For simulation of the resonant response of RF structures, the RF Module in COMSOL Multiphysics offers two reduced-order modeling techniques that can help overcome the need for long simulation times and extensive computational resources associated with traditional frequency domain analyses of resonant behavior, these methods are:
- Frequency-domain modal method
- Asymptotic waveform evaluation (AWE)
The frequency-domain modal method is best suited for quickly analyzing systems with multiple resonances in a defined frequency band. As a precursor to performing a frequency-domain modal analysis efficiently the results of an initial Eigenfrequency analysis must be refined to remove unwanted low frequency residues. The frequency-domain modal analysis is then applied with fine frequency stepping to define the multiple resonances.
In contrast, the AWE method is best used for analysis of smooth frequency responses containing a single resonance or no resonance. Therefore, it is extremely useful when simulating resonant circuits in which many frequency points need to be analyzed to resolve a single, narrow resonant response accurately. In this article we provide some background information on the AWE approach that will enable practicing simulation engineers to make effective use of AWE approaches for the evaluation of resonant behavior in RF systems.
Most of the frequency domain techniques used in computational electromagnetics result in a matrix equation which is solved at a single frequency. In the AWE technique, the Taylor series expansion around that frequency is applied to the matrix equation. Coefficients of the Taylor’s series are obtained in terms of the frequency derivatives of the matrices evaluated at the expansion frequency and are used to predict the frequency response of the system over a frequency range. AWE basically combines the fast-recursive moment method with the Padé approximation to compute poles and residues of truncated transfer functions. AWE was proposed in 1990 by Lawrence Pileggi from Carnegie Mellon University, its implementation in COMSOL Multiphysics is obtained in a special Adaptive Frequency Sweep study.
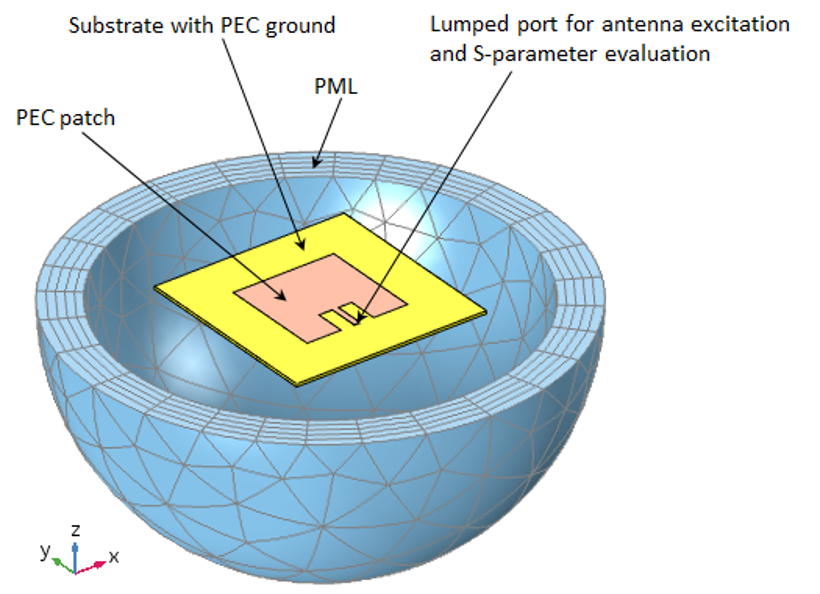
To see how it works, let’s consider the Microstrip Patch Antenna model from the COMSOL Application Library:
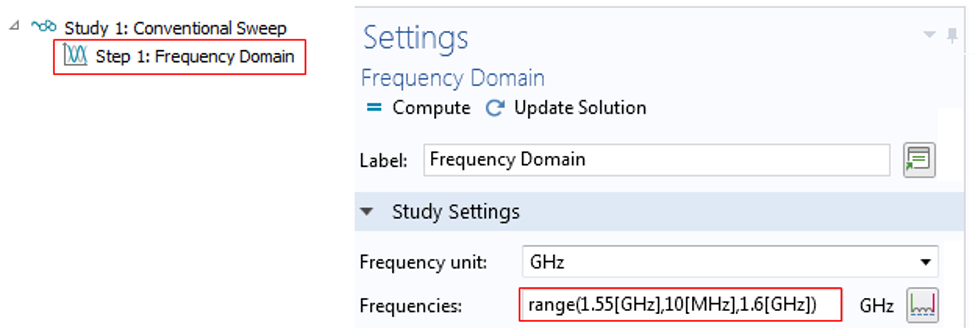
The study setup for a traditional frequency sweep from to in steps of is shown below:
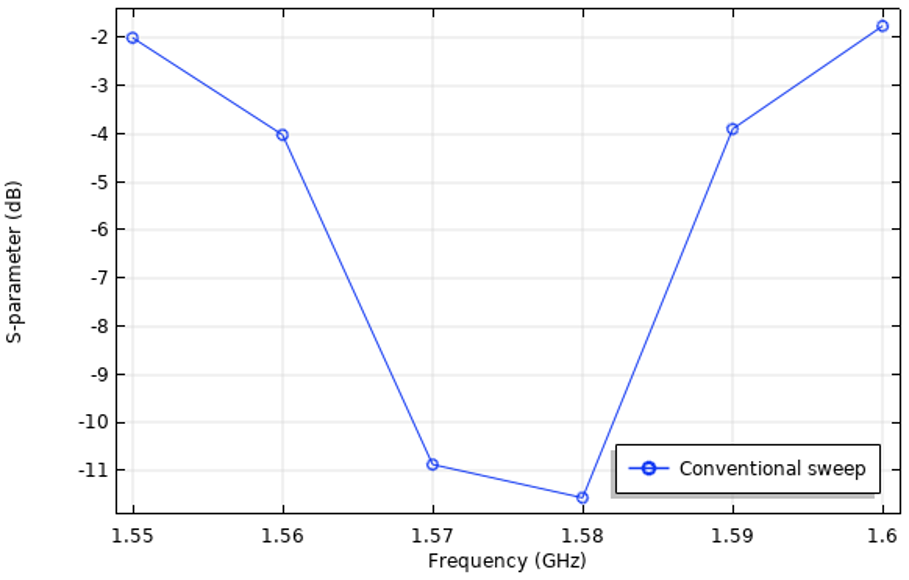
The resulting frequency response of the S-parameter of the microstrip patch antenna evaluated with a resolution is shown below:
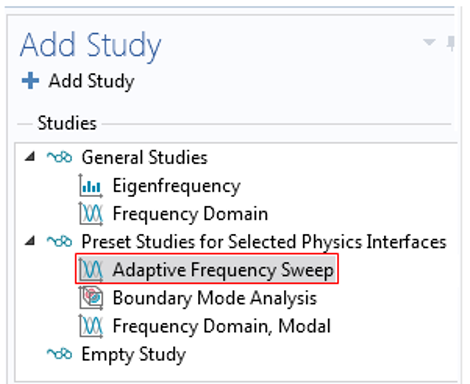
To improve the resolution of the S-parameter we need to perform a sweep with a resolution. Conventional frequency domain analysis approaches would require 100 times more CPU; alternatively, we can use the AWE methodology incorporated into the Adaptive Frequency Sweep approach available in the predefined frequency-domain study types:
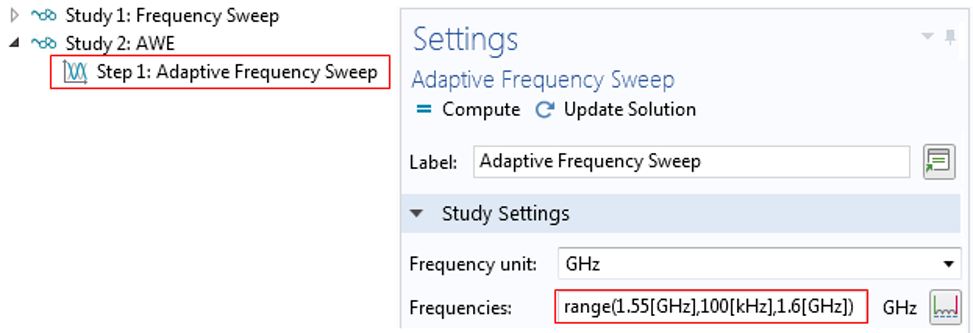
After adding the Adaptive Frequency Sweep study type, we must specify the same frequency range and include a frequency sampling step of :
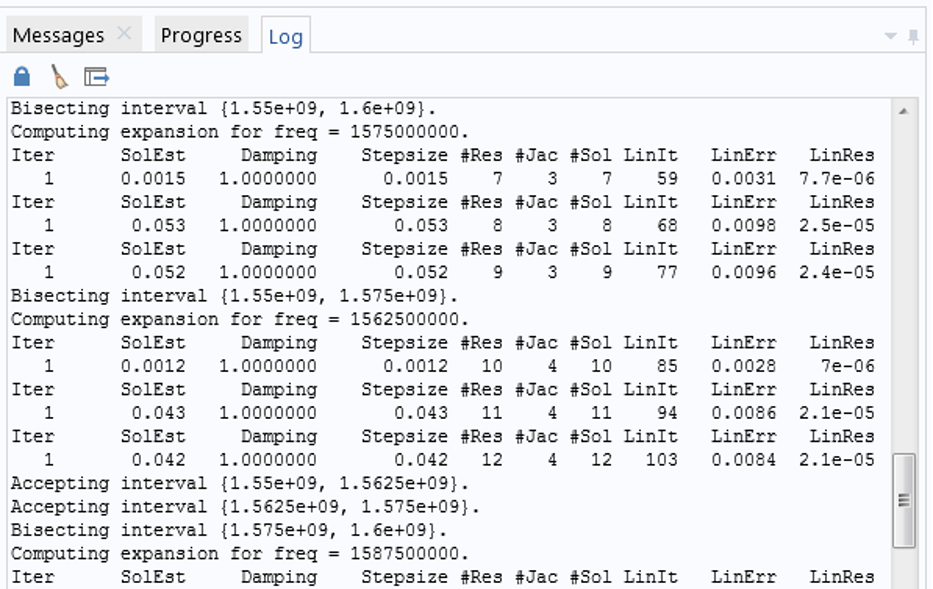
During the Adaptive Frequency Sweep study computation, we can observe the solver log which shows the Taylor series expansion performed around a few frequencies over the entire frequency range:
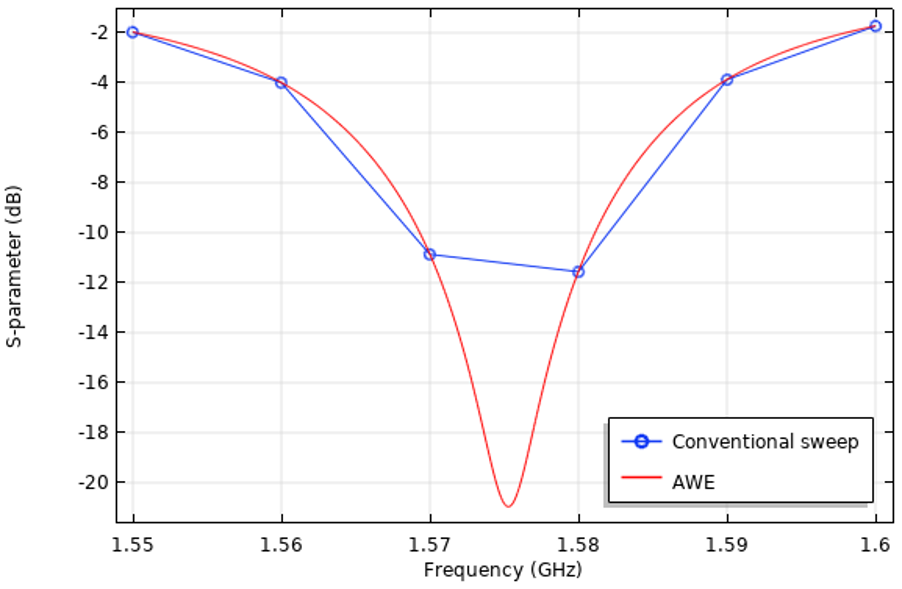
The resulting frequency response of the microstrip patch antenna is shown below and indicates the bandwidth wider than observed with the previous step:
The Table below summarizes the performance of AWE method using a 100 times finer frequency resolution. The AWE methodology uses only ~3 three times more CPU compared to the conventional frequency sweep with a coarse frequency resolution:
| Sweep method | DOFs | Frequency step | Number of sampling points | CPU |
| Conventional | 366,084 | 10 MHz | 6 | 2 min |
| AWE | 366,084 | 100 kHz | 501 | 4.5 min |
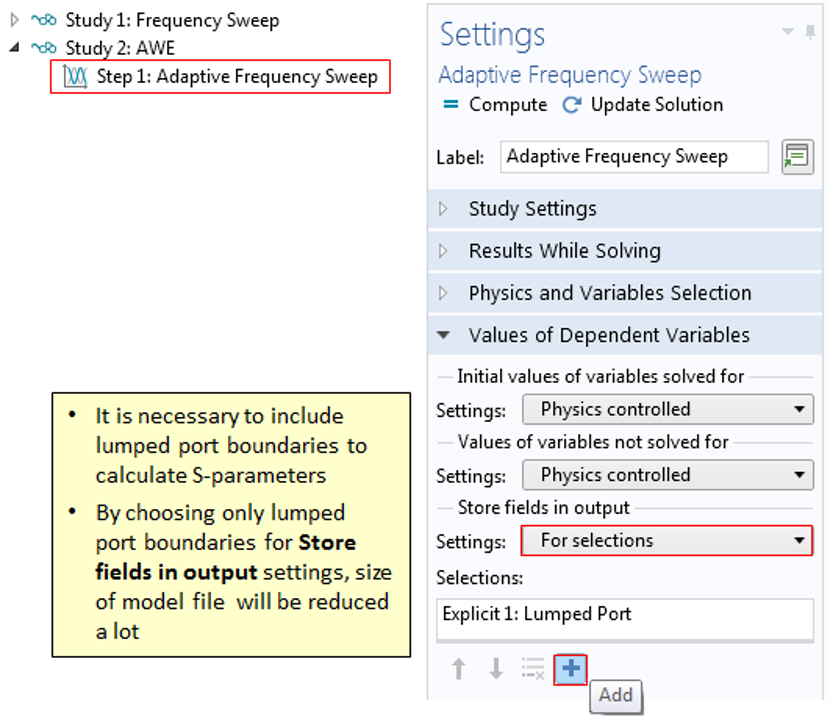
Through the AWE or frequency-domain modal method, we can observe the system response with fine increments in frequency and resolve resonant system response. These techniques provide a significant reduction in the amount of stored data compared to that generated by traditional frequency domain analyses with the same frequency resolution. Further reductions in the amount of stored data can be obtained by only storing data that is of direct relevance to the field of interest. In RF systems we are usually only interested in the S-parameters of the system response, and not in the data in the entire simulation domain. The data of direct interest is associated with the boundaries for S-parameter calculation, i.e. the lumped port and port boundaries. These boundary sizes are relatively small and thus we can reduce the file size of the stored data by running modal order reduction techniques and storing the solution only on the relevant port boundaries.
This can be achieved in two steps:
1. Use the Create Selection button for the Lumped Port boundary
- This creates the Explicit 1 selection for the antenna port boundary under the Component Definitions:
2. Use the above defined Explicit 1 selection to store the solution only on the port boundary:
For the example used here, storing only on the results on the port boundaries reduces the size of the mph file from about 3 GB to 3 MB.
Computationally, frequency-domain modal methods and AWE methodologies may increase the storage and CPU time requirements compared to a single frequency calculation. However, for a range of frequencies required to compute the resonant frequency response of a system, the frequency-domain modal and AWE techniques provides significant overall improvements in performance. When coupled with the use of modal order reduction techniques, the amount of data required to be stored to define the response of a resonant system can be significantly reduced.