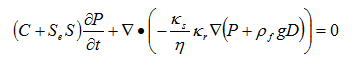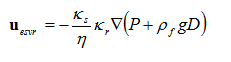Fluid Flow in Ceramic Matrix Composites
In a previous Blog we discussed some of the background to the production of Ceramic Matrix Composites (CMCs) using the Reactive Melt Infiltration (RMI) process. In this Blog we will address some of the issues associated with the first step in the process: infiltration of molten material into a porous preform.
Unsaturated flow through a porous media can be simulated using modified Richard’s and Darcy’s equation:
In this formulation, Darcy’s law provides the fluid velocity in the unsaturated media as:
For which:
The effective saturation, relative permeability, and moisture capacity are functions of pressure:
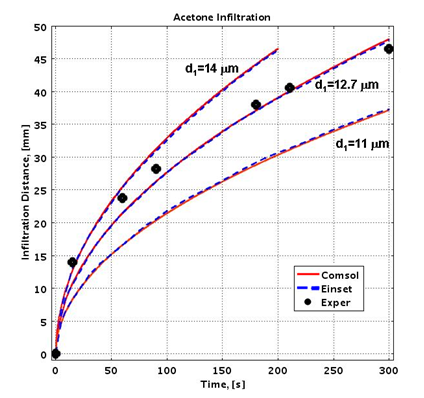
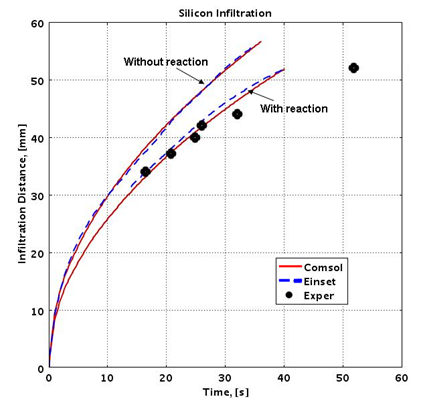
Results of the infiltration analysis show agreement with experimental results published by Einset for non-reactive flow (Figure 1) and reactive flow (Figure 2) in systems with different pore sizes.
Figure 1. Calculated and experimental acetone infiltration profiles for different pore diameter parameters.
Figure 2. Calculated and experimental infiltration profiles for silicon.
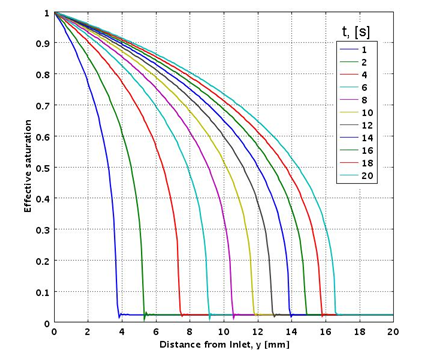
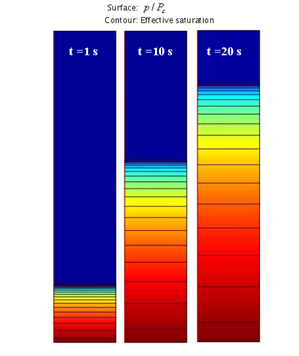
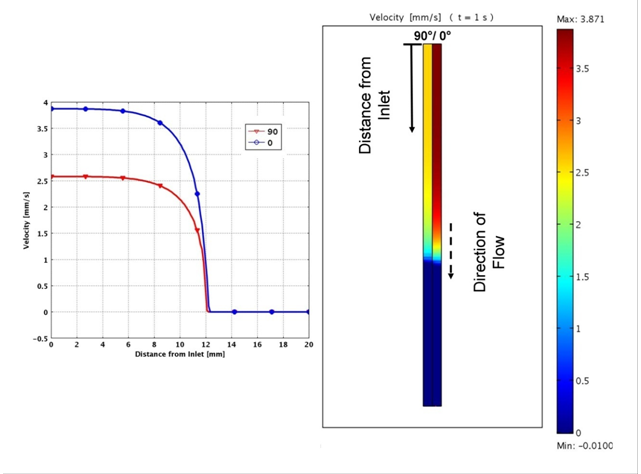
Once validated the analyses can predict other critical factors such as the flow front and its velocity during processing, examples are provided in 3 through 5.
Figure 3. Calculated saturation level as a function of infiltration time and distance from inlet.
Figure 4. Results of saturation during flow of Silicon into perform for infiltration times of 1s, 10s and 20s.
Figure 5. Distribution of the velocity in the fill direction for both layers at t= 1s.
The next blog in this series will consider the issues associated with the chemical reaction between infiltrating liquid and the porous preform, with specific focus on the infiltration of molten silicon into a porous carbon preform to produce a silicon carbide composite.