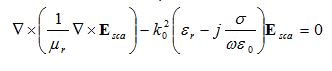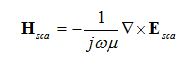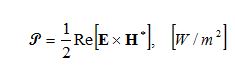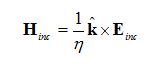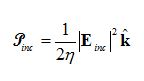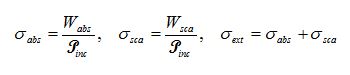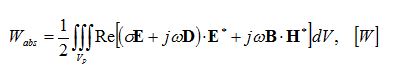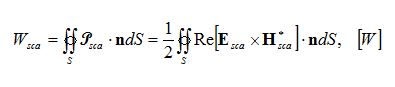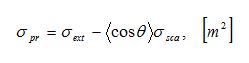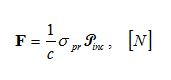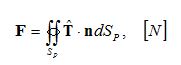Scattering of Electromagnetic Waves by Particles
Interaction between electromagnetic waves and particles produce unique scattering patterns that are wavelength and particle size dependent.
As electromagnetic waves propagate through matter they interact with particles or inhomogeneities and locally perturb the local electron distribution. This variation produces periodic charge separation within the particle causing oscillation of the induced local dipole moment, this periodic acceleration acts as a source of electromagnetic radiation thus causing scattering. The majority of the scattered wave oscillates at the same frequency as the incident wave and is termed elastic scattering. Interaction with the incident beam may also lead to absorption in the form of thermal energy. The combination of scattering and absorption attenuate the incident beam leading to extinction.
Scattering of electromagnetic waves by particles can be treated by two theoretical frameworks: Rayleigh scattering that is applicable to small, dielectric, non-absorbing spherical particles, and Mie scattering that provides a general solution to scattering independent of particle size. Mie scattering theory provide a generalized approach, has no particle size limitations and converges to the limit of geometric optics at large particle sizes. Consequently Mie scattering theory can be used to describe most scattering by spherical particles, including Rayleigh scattering, but due to the complexity of implementation, Rayleigh scattering theory is often preferred.
Rayleigh scattering is strongly dependent upon the size of the particle and the wavelength of the illuminating radiation. The intensity of the Rayleigh scattered radiation increases rapidly as the ratio of particle size to wavelength increases and is identical in the forward and reverse directions. The Rayleigh scattering model breaks down when the particle size becomes larger than approximately 10% of the wavelength of the incident radiation at which point Mie theory must be applied. The Mie solution is obtained through an analytical solution of Maxwell’s equations for the scattering of electromagnetic radiation by spherical particles in terms of infinite series rather than a simple mathematical expression.
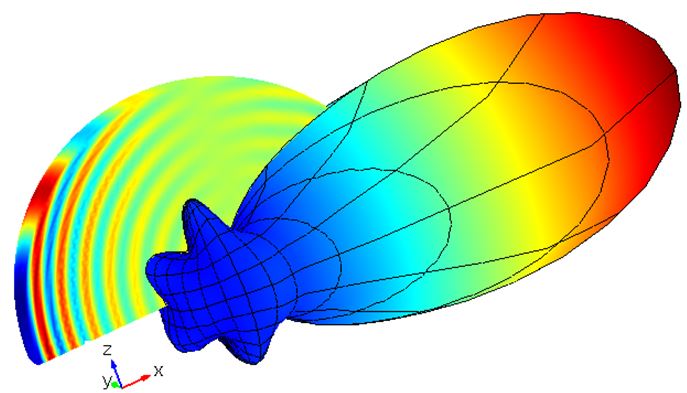
Mie scattering differs from Rayleigh scattering in several respects: it is roughly independent of wavelength and it is larger in the forward direction than in the reverse direction, figure 1. The greater the particle size, the more of the light is scattered in the forward direction. In addition to explaining many atmospheric effects of light scattering, applications of Mie scattering include environmental areas such as dust particles in the atmosphere and oil droplet in water as well as medical technology to measure cell nuclei in biological systems or measurement of collagen fibers in body tissue.
Analysis of Mie Scattering
Implementation of analytical solutions for Mie scattering by a particle or object is complex and requires solution of Maxwell’s equations to represent the incident, scattered and internal fields. These are not simple mathematical expressions and take the form of infinite series expansion of vector spherical harmonics that allows the cross sections, efficiency factors and distributions of intensity to be predicted. Further, the influence of particle geometry, incident of the incident wave and the particle’s material properties can be investigated.
In electromagnetic wave scattering problems, the total wave decomposes into the incident and scattered wave components:
Maxwell’s wave equation is solved with respect to scattered electric field:
and the scattered magnetic field is calculated from Faraday’s law:
The time-average Poynting vector for time-harmonic fields gives the energy flux:
For an incident plane wave, the magnetic field is related to the electric field by:
where is direction of the incident wave propagation, η = (μ/ε)1/2 is the characteristic impedance, ε is permittivity and μ is permeability of ambient medium. Hence, incident energy flux is calculated as
Important physical quantities can be obtained from the scattered fields. One of these is the cross section, which can be defined as the net rate at which electromagnetic energy (W) crosses the surface of an imaginary sphere centered at the particle divided by the incident irradiation. To quantify the rate of the electromagnetic energy that is absorbed (Wabs) and scattered (Wsca) by the particle, the absorption (σabs), scattering (σsca) and extinction cross sections are defined as:
The total absorbed energy is derived by integrating the energy loss over the volume of the particle:
The scattered energy is derived by integrating the Poynting vector over an imaginary sphere around the particle:
where n is unit vector normal to the imaginary surface S.
Due to the particulate nature of electromagnetic waves they also carry momentum and exert a force on the particle, called radiation pressure which can be obtained by integrating the Maxwell stress tensor over the surface of the sphere:
where σpr is the pressure cross-section, and <cosθ> is the asymmetry parameter.
The radiation pressure cross section can be used to calculate force which the particle experiences in the incident direction:
The total time-averaged force F acting on a particle illuminated with light can also be calculated using surface integral of the time-averaged Maxwell’s stress tensor :
Where Sp is surface enclosing particle volume Vp and n is unit normal vector to surface Sp.
In a following Blog we will demonstrate the implementation of Mie scattering into COMSOL Multiphysics and correlate the results with available analytical solution to simplified cases.