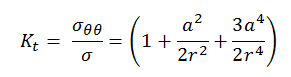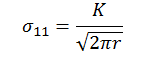The effect of loads on structures depends on the geometry and integrity of the structure, the materials and method of assembly of construction, and the type and rate of loading applied. Finite element analysis in structural mechanics ranges in complexity from linear-elastic, small deformation models to dynamic models that include temperature and rate effects. Simple isothermal linear elastic analyses are capable of determining the possibility of failure modes such as yielding or fatigue due to geometric discontinuities and/or connections.
To determine the effects of non-linear material properties on the structural mechanics of a design, non-linear finite element analysis can be conducted. Examples of this type of nonlinearity include plasticity in metals, hyperelastic, creep and viscoplasticity. Each of these material non-linearities may be included in finite element analysis in structural mechanics for loads that are quasi-static (i.e., do not produce inertial loading effects).
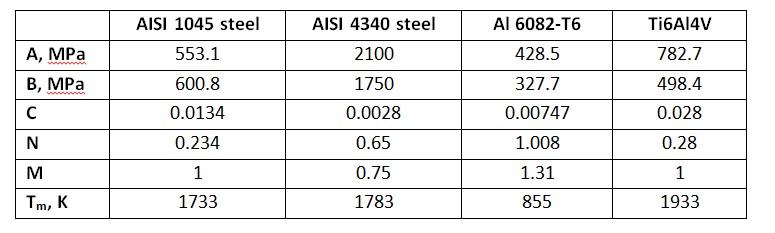
If the rate of change of load is small compared to the natural frequency, the response of the structure can be determined by a static structural mechanics analysis. For structures that are loaded at higher rates, inertial loading effects should be considered in the structural mechanics analysis. Examples of these types of loads include metal forming, blast and crash. Although high-rate loading and inertial effects can be included in finite element analysis in structural mechanics without the effects of non-linear material properties, high rate loads often produce nonlinear material effects. The dependence of material deformation of metallic materials on strain, strain rate and temperature are most often represented by the empirical Johnson-Cook model:
with typical values for selected alloys given below:
Thermomechanical Structural Mechanics
Many structures experience a combination of mechanical and thermal loads during operation. When a structure is constrained so that it cannot expand or contract as the temperature changes, large stresses can develop. Thermal strain develops due to temperature change based on the coefficient of thermal expansion of the material
Thermal strains do not produce stress in the structure. Thermal stress develops when the structure cannot expand to accommodate the thermal strains. For the full-constrained condition, thermal stress develops as
where E is the elastic modulus of the material. In many applications, thermal stresses can exceed the yield strength of the materials of construction and non-linear finite element methods are necessary to accurately calculate the stress within the structure.
Stress Concentration Effects
Most structures contain some geometric discontinuities, defects or cracks that produce local stress concentrations. The stress concentration factor, Kt, is defined as the ratio of the maximum local stress to a reference stress. For a circular hole of radius a in a plate under tensile stress, σ,the stress concentration factor is given by:
The maximum stress occurs at the edge of the circle, r=a, and a stress concentration factor of three is obtained for a circular hole with a radius much smaller than the surrounding structure. In contrast, for a sharp crack of length a, the stress at a distance r ahead of the crack tip is given by:
where the stress intensity factor is defined as. Thus, high stresses are produced at the tip of a crack that may locally exceed a material’s yield stress and cause plastic flow at low applied global stresses. For these reasons stress concentrations and cracks can lead to premature failure and their effects need to be included in a structural assessment of any engineering structure.
Fatigue in Structural Mechanics
Repeated loading and unloading over an extended period of time can cause fatigue failure where the lifetimes are probabilistic in nature and sensitive to a range of factors including the ratio of the minimum to maximum stress, temperature, environment, local geometry and residual stresses. The most commonly used treatments of fatigue consider three possible types of behavior:
- High cycle fatigue: Applied stresses are primarily elastic and failure occurs after ~104 to 106 cycles by accumulation of damage with continued loading. Behavior is characterized by S-N curves with some materials demonstrating a threshold stress below which failure does not occur.
- Low cycle fatigue (LCF): Failure occurs < ~104 cycles with stresses are sufficient to cause plastic deformation and is characterized by the empirical Coffin-Manson relationship:
Δεp/2 = εf.(2N)c
- Fatigue crack growth: Characterized by the relation between the cyclic stress intensity factor, ΔK, and crack growth rate shows three regimes of response:
- Unstable crack growth at high ΔKs
- Stable crack growth at intermediate ΔKs where da/dN = C. ΔKm and for metals 3<m<5
- Threshold behavior at da/dN ~ 107 mm/cycle where limited or no crack growth occurs
In addition to direct loading, real world structures may also be subject to loading as a consequence of the application. For example, thermal cycling can lead to the development of thermal stresses that may be sufficient to cause failure and resonant structural vibration may lead to fatigue failure.
AltaSim Technologies has successfully analyzed these loading conditions for the following industry sectors:
- Petrochemical processing plant
- Automotive manufacturing
- Aerospace
- Medical devices
- Telecommunications
- Defense and Homeland Security
Finite element method in structural mechanics using ABAQUS, COMSOL Multiphysics or LS DYNA has allowed our clients to identify the root cause of component failure, understand the implications of component design on structural operation, develop new designs and materials for extreme loading, define the expected lifetime of damaged components and develop inspection programs to maintain safe operation.
In addition, AltaSim also provides a comprehensive range of training on structural mechanics with the following courses:
Need Help with Structural Mechanics Analysis?
Contact us about our Structural Mechanics technology services.